Cómo detectar relaciones espurias con Python

Desde que el ser humano comenzó a observar el mundo, ha sentido la necesidad de entender por qué ocurren las cosas. Esta habilidad para identificar patrones y relaciones de causa-efecto es fundamental para el aprendizaje y la supervivencia. Sin embargo, también es una de nuestras mayores trampas cognitivas, pues a menudo nos lleva a conclusiones erróneas al asumir que, cuando dos cosas suceden juntas, una debe ser la causa de la otra.

---

Algunas correlaciones son tan absurdas que te harán dudar de todo

Antes de entrar en conceptos complejos, empecemos con una dosis de realidad humorística. A veces, dos variables muestran una relación estadística casi perfecta, pero la idea de que una causa la otra es simplemente ridícula. Estos ejemplos, conocidos como correlaciones espurias, son la prueba más clara de que una conexión numérica no significa nada sin una conexión lógica.

El extraño caso de Nicolas Cage y los ahogamientos en piscinas

Existe una correlación estadística casi perfecta entre el número de películas en las que aparece el actor Nicolas Cage cada año y el número de personas que se ahogan en piscinas en Estados Unidos. Este descubrimiento fue hecho por Tyler Vigen, un estudiante de derecho y criminología de Harvard. Al ver el gráfico, la mente busca una explicación. ¿La gente odia tanto a Nicolas Cage que cuando aparece en una película se ahogan en piscinas? ¿O es que el señor Cage celebra sus estrenos de una manera un tanto siniestra? La respuesta, por supuesto, es no. Se trata de pura coincidencia.

El misterio del gasto en ciencia y los suicidios

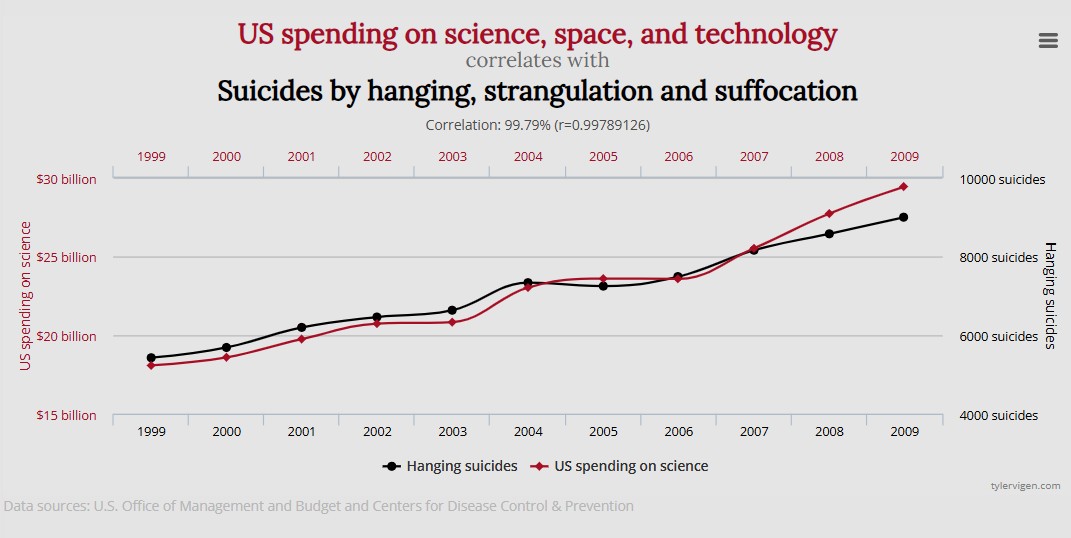
Otro ejemplo igualmente desconcertante muestra cómo, entre 1999 y 2009, la evolución del gasto del gobierno de EE. UU. en ciencia y tecnología fue prácticamente idéntica a la del número de suicidios por ahorcamiento. De nuevo, la relación estadística es fuerte, pero no hay ninguna razón lógica para pensar que una cosa causa la otra.

Estos ejemplos demuestran una lección fundamental: una correlación, por muy fuerte que parezca en un gráfico, no significa absolutamente nada por sí sola. Es solo el primer paso. Sin un mecanismo causal plausible, es simplemente ruido o una divertida coincidencia.

---

El verdadero culpable suele estar escondido: busca la “tercera variable”

La mayoría de las veces, cuando dos variables parecen estar relacionadas de forma lógica, el error no es tan obvio como en el caso de Nicolas Cage. A menudo, la conexión parece tener sentido, pero en realidad, ambas variables están siendo influenciadas por un “tercer factor” oculto, conocido en estadística como variable de confusión.

Ataques de tiburones y venta de helados

El ejemplo clásico es la fuerte correlación entre la venta de helados y los ataques de tiburón. Es fácil caer en la trampa de pensar que comer helado provoca estos eventos. Pero la causa real es una tercera variable que no estamos viendo: el clima cálido. Cuando suben las temperaturas, más gente compra helados y, al mismo tiempo, más gente va a la playa a nadar, lo que aumenta la probabilidad de encuentros con tiburones. El calor es el verdadero motor de ambas tendencias.

La luz y la miopía en niños

Otro caso fascinante es el de un estudio que encontró una correlación entre los niños que duermen con la luz encendida y el desarrollo de miopía. La conclusión parecía directa: dejar la luz encendida daña la vista. Sin embargo, un estudio posterior reveló al verdadero culpable: los padres miopes eran más propensos a dejar una luz encendida en la habitación de sus hijos, y la miopía tiene un fuerte componente genético. La luz no era la causa, sino un simple indicador de la verdadera causa: la genética.

La lección más importante es aprender a preguntarse siempre: “¿Qué otra cosa podría estar causando esto?”.

---

Esta confusión no es un juego: afecta tus decisiones diarias

Imagina que el tráfico de tu página web cae drásticamente justo cuando Google realiza una actualización de su algoritmo. La conclusión inmediata es culpar a la actualización. Sin embargo, puede que la verdadera causa sea una variable de confusión: esa misma semana coincidió con el inicio de unas vacaciones que alteraron el comportamiento de búsqueda de los usuarios (y puede que Google lo aprovechara para lanzar la actualización durante ese periodo). Atribuir la caída al algoritmo podría llevar a invertir tiempo y recursos en “solucionar” algo que no estaba roto, ignorando el verdadero factor.

Reconocer la diferencia entre la correlación y la causalidad es necesario para tomar decisiones informadas.

---

Entonces, ¿cómo demuestran los expertos la causalidad?

Si bien la intuición es útil, en el análisis de datos necesitamos herramientas más robustas. ¿Existe una fórmula para saber si una relación es real? La respuesta corta es que la estadística por sí sola no puede probar causalidad (eso requiere experimentación), pero sí puede ayudarnos a descartar correlaciones falsas mediante el control de variables.

La herramienta clave aquí es la Correlación Parcial.

La solución matemática: Controlando la tercera variable

Volvamos al ejemplo de los tiburones (X) y los helados (Y). Sospechamos que hay una tercera variable, la temperatura (Z), que es la verdadera causa de ambos.

Para comprobarlo, no nos sirve el coeficiente de correlación normal (Pearson). Necesitamos calcular la correlación entre X e Y eliminando matemáticamente la influencia de Z. Esto se hace con la fórmula de la correlación parcial. Empecemos:

• Variable A: Venta de helados
• Variable B: Ataques de tiburones.
• C (Variable de control): La temperatura ambiente.

La fórmula es esta:

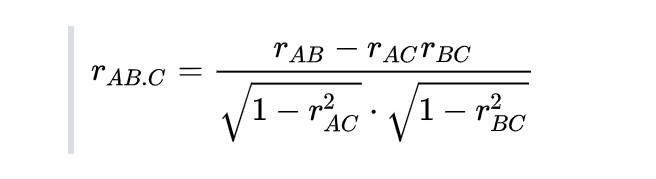
• rAB es el coeficiente de correlación convencional entre A y B.
• rAC es el coeficiente de correlación convencional entre A y C.
• rBC es el coeficiente de correlación convencional entre B y C

¿De donde salen las r? son los coeficientes de Pearson. Este valor oscila entre -1 y +1, así que toca calcularlo para cada par y aplicar la fórmula.

Interpretación del resultado:

• El numerador: Aquí está la clave. Restamos a la correlación original el producto de las relaciones con la temperatura. Si los helados y los tiburones solo se mueven por culpa del calor, el valor rAB será casi igual a rAC x rBC.
• El resultado: La resta dará cero (o un número muy cercano).

¿Qué significa el resultado?

• Si el resultado es casi 0: La relación era espuria. Al “quitar” la temperatura de la ecuación, la conexión entre helados y tiburones desaparece. Matemáticamente, hemos probado que no tienen nada que ver.

• Si el resultado sigue siendo alto: La relación es robusta. Significaría que, incluso en días fríos, la gente que come helado es atacada por tiburones (lo cual nos obligaría a buscar otra explicación científica).

¿Me tengo que aprender esta fórmula?

Como desarrolladores, no vamos a resolver esa ecuación a mano cada vez. En el ecosistema de Data Science, la librería estándar para esto es Pingouin.

Aunque Pandas es genial, no calcula correlaciones parciales de forma nativa. Pingouin sí, y además nos devuelve intervalos de confianza y significancia estadística (p-value) en una sola línea.

Si estás usando Google Colab, puedes probarlo ahora mismo con este bloque:

Si lo ejecutas en local, asegúrate de instalar las librerías:

pip install pingouin pandas

import pandas as pd
import pingouin as pg

# Simulamos datos
data = {
    'Helados':     [25, 31, 36, 38, 39, 49, 52], # Variable A
    'Tiburones':   [ 7,  8, 10, 10, 12, 12, 13], # Variable B
    'Temperatura': [20, 22, 24, 26, 28, 30, 34]  # Confusor C
}

df = pd.DataFrame(data)

print("--- Paso 1: Correlación ingenua (Pearson) ---")
# Calculamos la correlación directa ignorando el clima
corr_simple = df['Helados'].corr(df['Tiburones'])
print(f"Correlación aparente: {corr_simple:.4f}")  
# Debería ser alta, cerca de 1 (0.9369)

print("\n--- Paso 2: Correlación Parcial ---")
# Usamos Pingouin para 'limpiar' el efecto de la temperatura
# x: Helados
# y: Tiburones
# covar: Temperatura (la variable a eliminar)
resultado = pg.partial_corr(
    data=df, x='Helados', 
    y='Tiburones', 
    covar='Temperatura')

# Observa la columna 'r' en el resultado
print(resultado)
# Debería ser cercana a 0 (0.035)

Al ejecutarlo, verás que la columna r (correlación) se desploma, demostrando matemáticamente que la relación era una ilusión provocada por el clima.

La solución práctica: El Test A/B

En el entorno digital y el desarrollo de producto, rara vez nos paramos a calcular coeficientes parciales. La forma estándar de la industria para convertir correlación en causalidad es el Test A/B (o experimento controlado aleatorio).

Si observamos que “los usuarios que usan el modo oscuro gastan más dinero”, no asumimos causalidad. Diseñamos un experimento:

• Dividimos el tráfico aleatoriamente en dos grupos idénticos.
• A un grupo le forzamos el modo oscuro y al otro el claro.
• Si la diferencia de gasto persiste, entonces (y solo entonces) hemos encontrado causalidad.

Conclusión

La próxima vez que veas un gráfico con dos líneas subiendo juntas, hazte dos preguntas. Desde la lógica: “¿Existe un mecanismo que una estas dos cosas?”. Y desde la estadística: “¿Si controlo las variables externas, la relación desaparece?”.

Si no puedes responder afirmativamente, probablemente estés ante otro caso de Nicolas Cage y las piscinas.

Por favor, recuerda esto: correlación no implica causalidad.